Comme ceci est observé au cours de l’holocène, la température de la surface de la terre est assujettie à la résonance des ondes de Rossby gyrales qui résulte du forçage solaire et orbital. De ceci découle le caractère résonant du système climatique. Le forçage est d’autant plus efficace que sa période est proche d’une des périodes de résonance, ces dernières étant verrouillées en mode subharmonique (Pinault 2018d, 2020a, 2021a).

Durant l’ère glaciaire-interglaciaire les variations climatiques s’observent essentiellement à partir de l’analyse des carottes de glace prélevées dans les calottes glaciaires et les carottes de sédiments marins prélevées dans les fosses océaniques.
Sommaire
Les enregistrements des carottes de glace
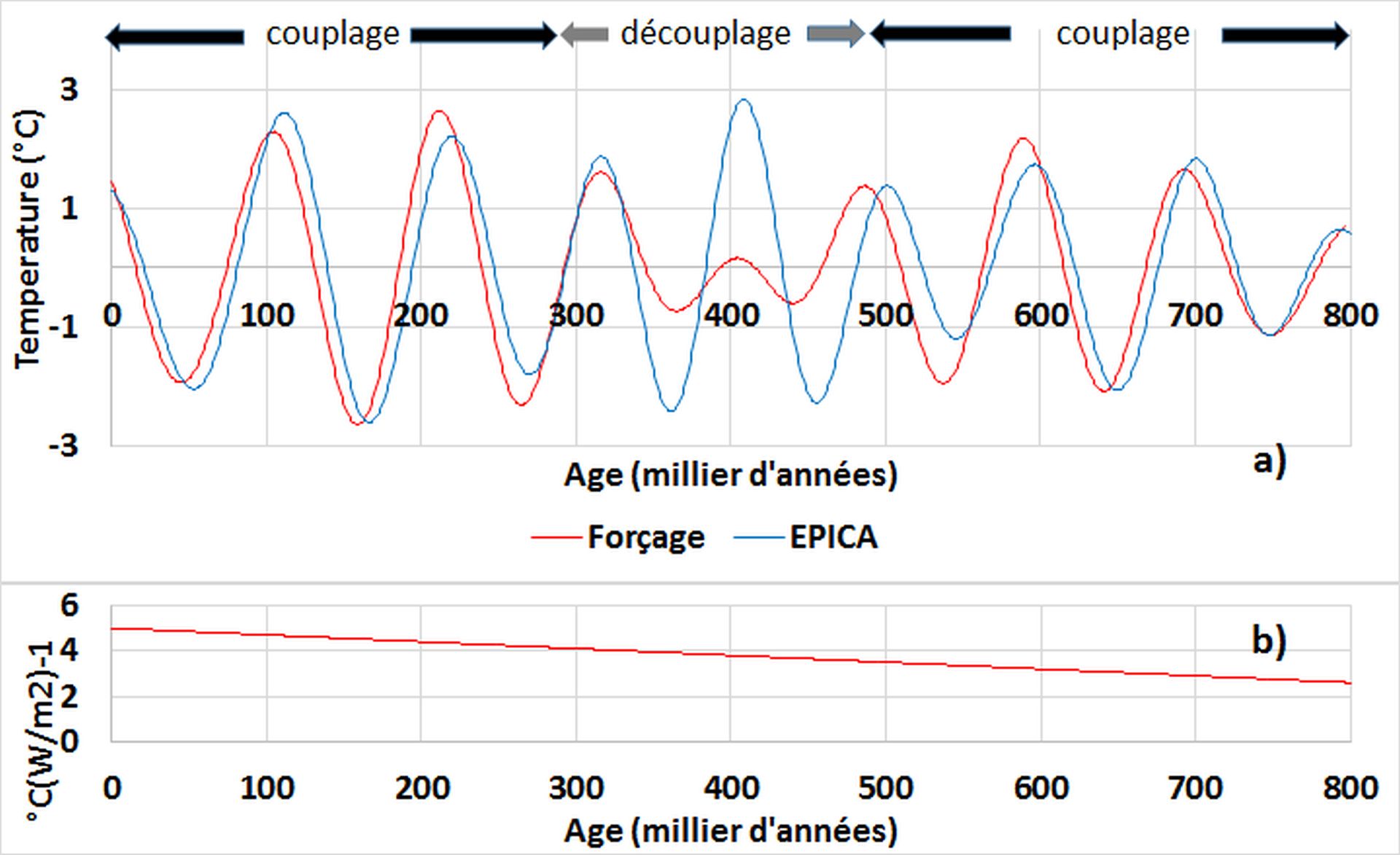
L’amplitude des variations orbitales de l’insolation et de la température moyenne globale estimée à partir d’EPICA [Augustin et al., 2004, Jouzel et al., 2007] montre que le couplage se produit principalement dans deux bandes centrées sur 41 Ka (obliquité) et 100 Ka (excentricité) [Pinault, 2018d].
En ce qui concerne l’excentricité, l’efficacité du forçage varie de manière significative au cours des 800 milliers d’années d’observation, augmentant progressivement de 2,6 à 4,0 °C(W/m2)-1. Le couplage se relâche entre 450 et 350 Ka BP quand le forçage s’effondre, puis récupère lorsque l’amplitude du forçage augmente à nouveau. La stabilité de l’oscillation de l’onde de Rossby gyrale, qui se poursuit même lorsque le forçage s’évanouit en raison de la rémanence des forces géostrophiques à grande échelle, donne à penser qu’elle est l’onde fondamentale pour les grandes périodes, c’est à dire l’onde dont l’amplitude est directement assujettie à l’influence du forçage orbital. L’augmentation de l’efficacité du forçage reflète le fait que la période du forçage orbital et la période propre des ondes de Rossby gyrales se rapprochent au cours du temps.

Cette onde fondamentale produit deux harmoniques dont les périodes propres sont 49,2 et 24,6 Ka, l’une et l’autre glissant vers la période de forçage liée à l’obliquité et la précession suite à la dérive de la latitude des centroïdes. L’harmonique lié à l’obliquité subit des instabilités révélées par les variations de l’efficacité du forçage orbital.
Ceci confirme que la latitude de la composante de période 49,2 Ka ne diffère pas de celle du gyre de 2°30′ de façon constante, mais elle oscille autour de la valeur centrale, l’efficacité maximale étant atteinte lorsque la composante se confond avec le gyre. En effet, l’avance et le recul successifs du front polaire ne peuvent être invoqués pour expliquer les changements soudains dans l’amplitude des deux harmoniques parce que la dynamique de la banquise polaire est beaucoup plus rapide que ce qui est observé ici, d’après ce que nous avons vu au cours de l’Holocène : quelques milliers d’années par rapport à près de 50 Ka.

Les variations orbitales liées à la précession forcent l’onde de Rossby gyrale de période 24,6 Ka. L’efficacité du forçage est soumise à de fortes variations d’amplitude, en relation avec la phase de l’onde fondamentale comme cela se produit 451, 332, 242, 127, 9 Ka BP: les amplitudes maximales sont atteintes lorsque l’onde fondamentale croit.
Il semble que la composante de période 393,2 Ka ne soit pas couplée avec l’oscillation de l’excentricité de période 400 Ka, bien que plus intense que celle de période 100 Ka. La seule raison plausible semble résulter de l’écart entre les deux périodes, plus de 30 Ka actuellement. Enfin, la somme des trois composantes explique assez bien la température moyenne globale de la période glaciaire-interglaciaire au cours des 800 Ka d’observation.
Les enregistrements des carottes de sédiments
La transition du milieu du Pléistocène (MPT)
Les enregistrements des carottes de sédiments [Lisiecki et Raymo, 2005] permettent d’élucider ce qui s’est produit il y a 1,25 Ma (Ma=106 années) lorsque la période dominante de la température moyenne globale a sauté de 41 à 100 Ka. En effet, lorsque la température est étalonnée par rapport aux enregistrements des carottes de glace, les carottes de sédiments peuvent être utilisées d’une manière quantitative sur l’intervalle 0-2 Ma BP au cours duquel la diffusion, qui a tendance à brouiller le signal utilisé pour l’estimation des variations de température, c’est à dire δ18O dans les foraminifères, peut être négligée.

La période de l’excentricité ~100 ka a varié au cours du quaternaire, la période se rapprochant de la période de résonance entre 1200 et 1300 ka (Figure 5).
Le proxy de température globale, qui est déduit de δ18O dans les foraminifères des carottes de sédiments, est comparé à la température modélisée T obtenue de telle sorte que T=SI×Sensibilité où l’irradiance solaire SI obtenue à partir des calculs et le proxy de température T sont filtrés dans des plages de périodes associées aux modes subharmoniques n10 (Figure 6a) et n11 (Figure 6b). Les sensibilités, qui sont représentées dans la Figure 6c, sont ajustées par un polynôme de degré 3 défini de telle sorte que l’erreur quadratique moyenne entre les températures observées et modélisées soit minimale (Figure 6a, b).
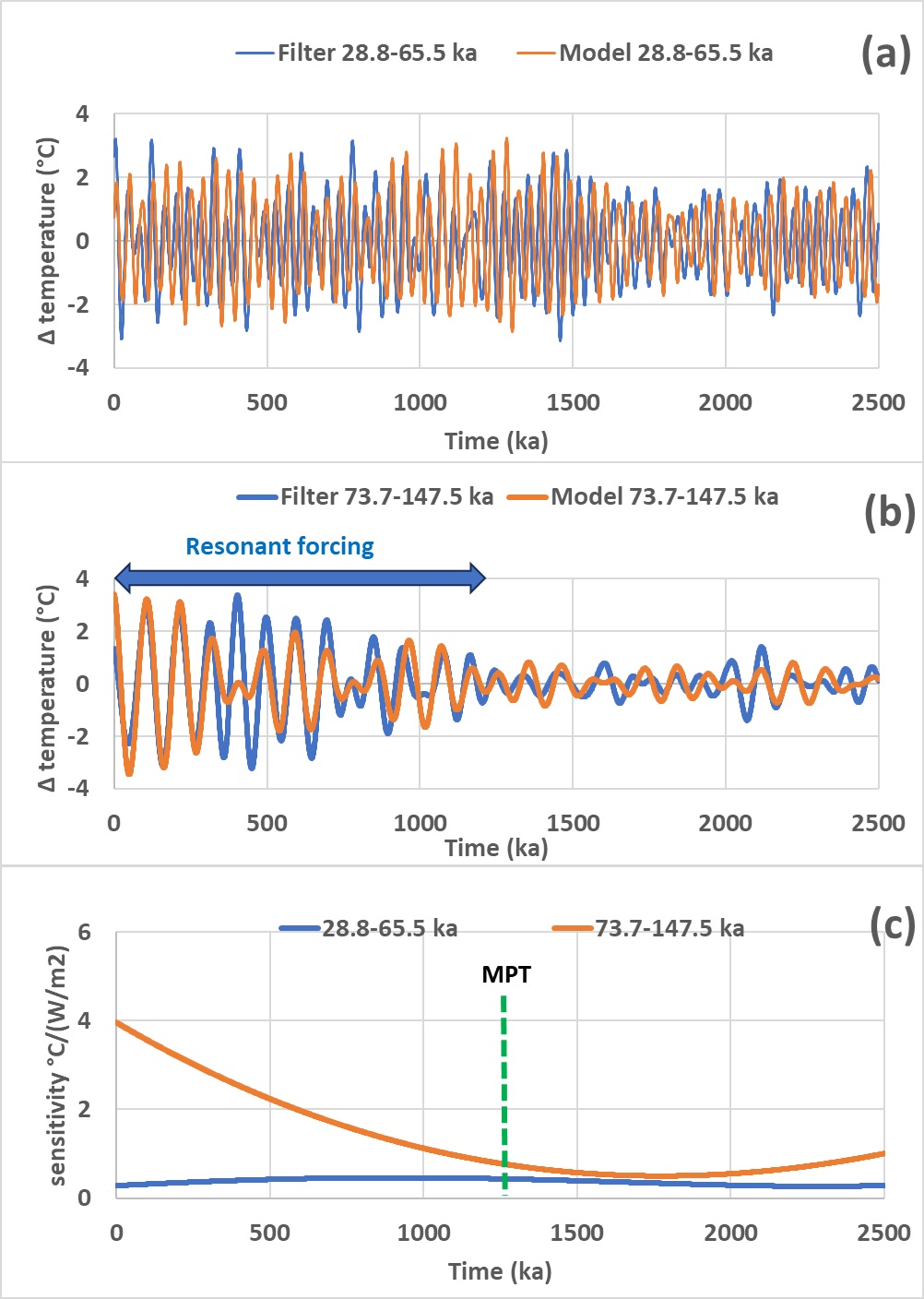
La sensibilité climatique dans la plage de périodes 73,7 – 147,5 ka encadrant la période d’excentricité de 98 ka met en évidence une résonance dont l’accord est pointu, reflété par sa croissance rapide et quasi-linéaire depuis 1250 ka. Elle atteint actuellement 4,0 °C(W/m2)-1, suggérant que l’accord est encore en cours d’amélioration. La période d’excentricité (Figure 5) est proche de la période de résonance qui, pour le mode subharmonique n11, est de 98,3 ka.
Concernant la sensibilité climatique à l’obliquité, elle reste quasiment constante durant la période d’observation, soit 2500 ka, ce qui montre que la MPT n’a pas d’influence sur la réponse de l’onde gyrale dont le mode subharmonique est n10. La période moyenne d’obliquité, soit 41,1 ka (Figure 1), est loin de la période naturelle la plus proche des ondes gyrales, soit 49,2 ka, qui suppose que le système multifréquence des ondes gyrales a atteint sa stabilité optimale. D’après la relation de dispersion, le centroïde de l’onde gyrale doit être décalé de 0,8° vers l’équateur pour que sa période naturelle fusionne avec la période de forçage. La sensibilité climatique, stable durant la période d’observation, reste inférieure à 0,45 °C(W/m2)-1, ce qui révèle un accord de mauvaise qualité entre le forçage et les périodes propres.
Depuis près de 1,25 Ma, la quasi-coïncidence de la période de forçage de l’excentricité et de la période naturelle de l’onde gyrale de mode subharmonique n11 fait que l’excentricité a pris le pas sur l’obliquité malgré la faible amplitude des modulations d’irradiance solaire liées à l’excentricité par rapport à celle liée à l’obliquité (Figure 1).
Une autre transition s’est produite il y a 2,38 Ma
Une autre transition s’est produite il y a 2,38 Ma, la Transition au Quaternaire Précoce (EQT), impliquant des périodes de forçage 10 fois plus longues que lors de la MPT. Cette transition est mise en évidence en considérant les plages de périodes 295-590 ka et 590–1180 ka associées aux modes subharmoniques n13 et n14, afin d’encadrer les périodes de forçage d’excentricité dont les périodes moyennes sont de 408 ou 786 ka (Figure 1). Ici encore, l’irradiance solaire SI obtenue à partir des calculs, multipliée par la sensibilité climatique est comparée à la température globale observée, obtenue à partir de Lisiecki et Raymo, filtrée dans les plages de périodes pertinentes.
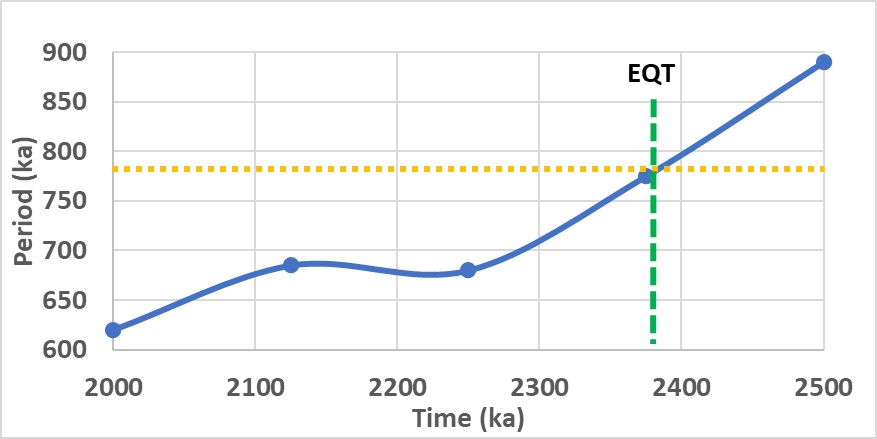
Comme pour la MPT, un glissement de la période de forçage s’est produit, mettant en résonance le mode subharmonique n14 sous l’effet de l’excentricité dont la période est de 786 ka (Figure 7).
La sensibilité climatique au forçage radiatif obtenue en minimisant l’erreur quadratique moyenne entre les séries observées et calculées, filtrées dans les plages de périodes 295-590 ka (Figure 7a) et 590–1180 ka (Figure 7b) montre que les variations de la température globale anticipent celles de SI de 100 ka et 180 ka, respectivement. La cause de cet écart, qui augmente avec la période, résulte probablement de biais résiduels attribuables aux processus de diagenèse qui subsistent après suppression de la tendance des données.

Comme le montre la Figure 8c, la sensibilité climatique dans la plage de périodes 590–1180 ka a atteint un maximum à 3,5 °C(W/m2)-1 il y a près de 0,8 Ma, ce qui est considérable puisque cette valeur est comparable à celle atteinte dans la plage de périodes 73,7–147,5 ka encadrant la période d’excentricité de 98 ka (Figure 6c). Cette lente oscillation de température a donc un impact significatif sur le bilan énergétique de la seconde moitié du Quaternaire avec une baisse de température de 2 °C entre 1,2 Ma et 0,8 Ma, puis une hausse de 2 °C entre 0,8 Ma et 0,4 Ma.
La sensibilité climatique dans la plage de périodes 295-590 ka encadrant la période d’excentricité de 408 ka reste faible, près de 0,5 °C(W/m2)-1, et stable. Ici encore, cela révèle un accord de mauvaise qualité entre le forçage et les périodes propres, et qui est resté insensible à l’EQT. L’ajustement du mode subharmonique n13 à la période de forçage n’a nécessité qu’un déplacement de 0,2° vers le pôle du centroïde de l’onde gyrale pour augmenter la période de 0,39 à 0,41 Ma (Figure 1).
Forçage résonant des ondes gyrales
Les propriétés du système dynamique constitué d’ondes de Rossby gyrales multifréquences autour des gyres subtropicaux océaniques reposent sur un modèle physique simple qui suppose que ces ondes se comportent comme des oscillateurs inertiels couplés. La formulation des 15 premières périodes propres des ondes gyrales suppose que ce système dynamique est à l’équilibre. Cela signifie qu’au fil du temps, chaque oscillateur transmet aux autres oscillateurs autant d’énergie de couplage qu’il en reçoit.
En fait, ce système dynamique est la plupart du temps hors d’équilibre car les périodes et les amplitudes des cycles orbitaux varient au cours du temps. De plus, la réponse de ce système inertiel est très étalée dans le temps tout en restant aussi proche que possible de l’équilibre, ce qui assure sa pérennité.
Comme le montrent les figures 6c et 8c, l’efficacité du forçage orbital augmente au cours du temps une fois les ondes gyrales de modes subharmoniques n11 et n14 entrées en résonance. Ce caractère inertiel persiste après que la période de forçage s’est éloignée de la période de résonance comme le montrent les figures 5 et 7. Qu’il s’agisse de MPT ou d’EQT, l’augmentation de l’efficacité du forçage orbital après la transition implique le réarrangement du système dynamique vers sa configuration d’équilibre en accord avec les nouvelles conditions de résonance.
Dans le cas de la MPT, l’efficacité du forçage dans la plage de périodes 73,7 – 147,5 ka continue d’augmenter actuellement. Ceci peut s’expliquer par le fait qu’avant la MPT, le centroïde de l’onde gyrale de mode subharmonique n10 avait glissé de 0,8° vers l’équateur pour s’accorder au cycle orbital de période 41 ka alors que la période propre de l’onde gyrale est de 49 ka. Le système dynamique est resté hors d’équilibre pour s’adapter au mieux au cycle d’obliquité dont l’amplitude est supérieure à celle du cycle d’excentricité à 98 ka. Pendant la MPT, l’accord parfait entre la période d’excentricité et la période propre de l’onde gyrale de mode subharmonique n11 a modifié les conditions de résonance. Le centroïde de l’onde gyrale de mode subharmonique n10 a dû revenir à sa position d’équilibre en glissant de 0,8° vers le pôle. Ce réarrangement du système dynamique est toujours en cours car la configuration d’équilibre n’a pas encore été atteinte.
Dans le cas de l’EQT, l’efficacité du forçage dans la plage de périodes 590–1180 ka a atteint un maximum il y a environ 0,8 Ma et n’a cessé de diminuer depuis. Ceci peut s’expliquer par le fait qu’avant l’EQT le centroïde de l’onde gyrale de mode subharmonique n13 avait glissé de 0,2° vers le pôle pour s’accorder au cycle orbital de période 408 ka alors que la période propre de l’onde gyrale est de 393 ka. Le système dynamique est resté hors d’équilibre pour s’adapter au mieux à ce cycle d’excentricité dont l’amplitude est plus grande que celle du cycle à 786 ka. Pendant l’EQT, l’accord parfait entre la période d’excentricité et la période propre de l’onde gyrale de mode subharmonique n14 a modifié les conditions de résonance. Le centroïde de l’onde gyrale de mode subharmonique n13 a dû revenir à sa position d’équilibre en glissant de 0,2° vers l’équateur. Le réarrangement du système dynamique s’est poursuivi jusqu’à ce que l’efficacité du forçage atteigne un maximum il y a 0,8 Ma, alors que la configuration d’équilibre n’avait pas encore été atteinte. Ensuite, l’écart croissant entre la période de forçage et la période propre de l’onde gyrale de mode subharmonique n14 a de nouveau favorisé la prédominance du mode subharmonique n13, en raison de la plus grande amplitude du cycle orbital à 408 ka par rapport à celui à 786 ka. La diminution de l’efficacité du forçage montre que le réarrangement du système dynamique est toujours en cours. Cela se poursuivra jusqu’à ce qu’une valeur stable de l’efficacité du forçage soit atteinte. Le système dynamique restera hors d’équilibre jusqu’à ce que les conditions de résonance soient modifiées.
Le fonctionnement du système dynamique suggère une forte interaction entre les deux ondes gyrales de modes subharmoniques consécutifs comme c’est le cas des modes n10 et n11, ainsi que n13 et n14. En revanche, cette interaction disparaît lorsque l’écart entre les modes subharmoniques augmente, ce qui explique l’apparente indépendance des deux transitions, la MPT et l’EQT.
La dernière glaciation
En ce qui concerne la dernière glaciation dans la plage de périodes 73,7 – 147,5 ka encadrant l’excentricité de période 98 ka, le forçage orbital a atteint un maximum il y a 103 ka et un minimum il y a 50 ka (Figure 9). La température globale, qui est presque en phase avec le forçage orbital, est à son maximum lorsque la pycnocline s’approfondit et à mi-chemin entre son niveau le plus bas et le plus haut. L’accélération du courant polaire du gyre dans la direction anticyclonique atteint également son maximum tandis que celle du courant radial s’annule, conformément aux équations de mouvement des ondes de Rossby gyrales. Les échanges de chaleur océan-atmosphère sont favorisés à la fois par 1) l’accélération du WBC dans le sens anticyclonique, qui favorise les échanges de chaleur entre les tropiques et les hautes latitudes, et 2) l’approfondissement de la pycnocline, qui favorise les processus convectifs et évaporatifs et l’évacuation de la chaleur latente. D’autre part, la disparition du courant radial favorise le confinement des échanges thermiques le long du gyre.
Ainsi, l’accélération du WBC a atteint un maximum dans le sens anticyclonique il y a 103 ka, puis s’est inversée il y a 78 ka (un quart de période correspond approximativement à 25 ka). La pycnocline a atteint son niveau le plus bas (la perturbation de la hauteur de surface son niveau le plus haut) lorsque l’accélération du courant radial a atteint son maximum, orientée vers l’extérieur du gyre, ce qui a favorisé la dissipation de chaleur hors du gyre. L’accélération du WBC a atteint un maximum dans le sens cyclonique il y a 50 ka, avec la disparition du courant radial. La phase de glaciation a alors été la plus active car les échanges de chaleur entre les tropiques et les hautes latitudes étaient minimes. La pycnocline était dans sa phase ascendante, à mi-chemin de son parcours, ce qui a réduit les échanges océan-atmosphère. L’accélération du WBC s’est inversée il y a 25 ka alors que l’accélération du courant radial était orientée vers le gyre. L’accélération du WBC est sur le point d’atteindre un maximum dans le sens anticyclonique aujourd’hui. La phase de déglaciation est alors la plus active car les échanges de chaleur entre les tropiques et les hautes latitudes sont maximaux. La pycnocline est dans sa phase descendante, à mi-chemin de son parcours, ce qui favorise les échanges océan-atmosphère.

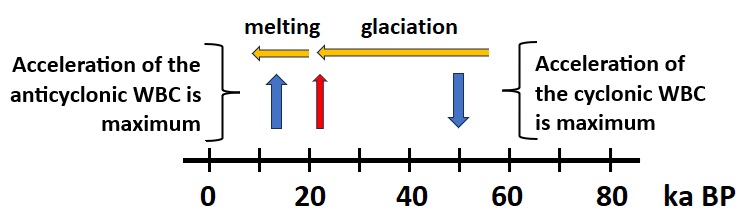
La rétroaction de la réponse du Gulf Stream au forçage orbital est d’autant plus forte que le gradient thermique de l’eau de mer au-dessus de la thermocline entre les hautes et basses latitudes du gyre est important, ce qui est une conséquence de l’avancée de la calotte glaciaire arctique. Cela a pour effet d’accélérer encore davantage le courant géostrophique du gyre (qui s’écoule de manière anticyclonique), ce qui accroit le transfert de chaleur des basses latitudes vers les hautes latitudes du gyre, comme ceci s’est produit à la fin de la période glaciaire.

Ceci explique la forte asymétrie observée entre les périodes glaciaires et interglaciaires (Figures 10 et 11). La limite sud de la calotte glaciaire a été atteinte il y a près de 21 ka, soit près de 30 ka après que l’accélération du courant de bord ouest a été minimale alors que le cycle complet de déglaciation n’a duré que 25 à 30 ka.
Cette nouvelle approche montre comment les calottes polaires et les accélérations du courant de bord ouest interagissent en synergie lors des périodes de glaciation/déglaciation. Ce couplage est particulièrement fort dans l’Atlantique Nord en raison de l’avancée du Groenland. La circulation thermohaline agit essentiellement comme un débordement. Les principaux moteurs des courants polaires modulés des gyres ainsi que du courant de dérive sont les forces géostrophiques, c’est-à-dire la force de Coriolis et la gravité, dont l’action est renforcée par la rétroaction positive induite par le gradient thermique entre les basses et hautes latitudes des gyres, qui est étroitement contrôlé par l’avancée/retrait des calottes glaciaires.
Problèmes ouverts résolus
La plupart des problèmes ouverts concernent la sélectivité de la sensibilité climatique au forçage orbital en fonction de la période, ce qui nous ramène au problème des transitions. Ces observations, incompatibles avec la théorie standard de Milankovitch, trouvent une explication simple lorsque les gyres subtropicaux sont censés médiatiser la réponse climatique. Du fait de l’inertie des courants géostrophiques polaires et radiaux des gyres subtropicaux, la phase de réchauffement peut précéder l’augmentation de l’insolation, dont la période peut varier de manière significative comme le montre la largeur des pics de l’irradiance solaire dans le spectre de Fourier (Figure 1).
Référence
Berger, A.; Loutre, M.-F. Insolation values for the climate of the last 10 million years. Quat. Sci. Rev. 1991, 10, 297–317.
Lisiecki, L.E. and Raymo M.E. (2005) LR04 Global Pliocene-Pleistocene Benthic d18O Stack. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series #2005-008. NOAA/NGDC Paleoclimatology Program, Boulder CO, USA.
Glossaire
Les événements de Heinrich, qui furent décrits pour la première fois par le géologue et océanologue Hartmut Heinrich, se sont produits pendant la dernière période glaciaire. Au cours de ces événements, de nombreux icebergs se sont détachés des glaciers et ont traversé l’Atlantique Nord. Les icebergs contenaient des masses rocheuses érodées par les glaciers, et lors de leur fusion, la matière a été abandonnée sur le plancher océanique en tant que « débris ayant voyagé sur un radeau de glace ».
Les événements Dansgaard-Oeschger (souvent abrégés D-O) désignent les fluctuations rapides du climat qui ont eu lieu au cours de la dernière période glaciaire.
L’onde quasi-stationnaire fondamentale est en phase avec le forçage. Dans les tuyaux sonores, les cordes et les membranes vibrantes se forment des harmoniques dont la période est un diviseur de celle de l’onde fondamentale. Pour ce qui concerne les longues vagues océaniques, il se forme des subharmoniques dont la période est un multiple de celle de l’onde fondamentale comme ceci se produit pour les modes baroclines d’ordre élevé.