Sommaire
Forçage radiatif
L’effet de serre (ou forçage radiatif) résulte de la basse température des couches supérieures de la troposphère, comparée à la température de la surface de la terre. Le système terre-atmosphère ne connaîtrait pas, en effet, l’effet de serre s’il était isotherme, émettant dans son ensemble dans le spectre infra-rouge comme le ferait un corps noir.
L’effet de serre augmente la température de surface de la planète en réduisant les pertes d’énergie vers l’espace dont la température est proche du zéro absolu (2,7 K) par absorption des infrarouges émis par la terre. Cette absorption se fait principalement par la vapeur d’eau dans les couches basses de l’atmosphère, chaudes et humides, et par le CO2 dans les couches hautes, froides et sèches.
Le rôle des gaz à effet de serre tels que le méthane (CH4) ou l’ozone (O3) est bien compris, l’absorption des infrarouges émis depuis la surface de la terre dans les bandes d’absorption de ces gaz dépendant directement de leur concentration dans l’atmosphère. Par contre, cette relation de causalité est beaucoup plus subtile pour le CO2 en raison du phénomène de saturation qui fait que, en première approximation, l’absorption des infrarouges émis par la terre n’augmente pas avec sa concentration. Mais ceci n’est pas tout à fait vrai pour deux raisons :
- La raie d’absorption du CO2 située entre 14 et 17 µm n’est pas saturée sur ses ailes : l’absorption augmente donc faiblement avec la concentration du CO2
- L’altitude à partir de laquelle le rayonnement thermique s’échappe vers l’espace augmente avec la concentration de CO2 en raison de l’épaississement de la couche opaque au sein de laquelle toute émission dans le spectre infrarouge du CO2 est réabsorbée ou diffusée. La température diminuant avec l’altitude, l’émission est plus faible, ce qui renforce le forçage radiatif de l’atmosphère.
Il y a lieu de souligner le rôle particulier joué par la vapeur d’eau sur le climat : le mécanisme invoqué pour expliquer la température clémente de notre planète, qui devrait être de -18°C en l’absence de tout effet de serre, lui est principalement attribué. La convection thermique redistribue l’humidité et homogénéise la température dans la couche de 0 à environ 4,4 km. Ceci influence l’équilibre thermique vertical de la planète en amenuisant la diminution moyenne de température avec l’altitude que l’effet de serre impose à la troposphère. Sans les mécanismes convectifs, le changement serait plus abrupt et donnerait une température moyenne de la surface terrestre plus élevée. En s’évaporant des océans la vapeur d’eau prélève de l’énergie, la chaleur latente, qui est libérée lors de sa condensation dans l’atmosphère. Le réchauffement qui en résulte limite les phénomènes de convection depuis la surface de la terre, réduisant ainsi les échanges thermiques vers la haute atmosphère. A ceci s’ajoute l’action des nuages bas qui ont un fort effet d’albédo et les nuages hauts dont l’effet de serre est important.
Équilibre énergétique
Le lien entre le réchauffement et l’augmentation de la concentration du dioxyde de carbone atmosphérique depuis le début de l’âge industriel est mal compris.Une rétroaction positive de la vapeur d’eau suite à l’augmentation de température amplifie l’impact des gaz à effet de serre. La boucle de rétroaction fait intervenir les océans à la fois en tant que pourvoyeurs de vapeur d’eau mais également par leur effet modérateur de la température de surface des continents. D’autre part au réchauffement anthropique se superpose la variabilité naturelle du climat qui, jusqu’à présent, restait hautement spéculative.
A l’équilibre thermique, l’énergie solaire reçue par la terre est égale à l’énergie thermique réémise dans l’espace sous forme de rayonnement infrarouge. En écrivant que le Flux infrarouge émis = Flux solaire absorbé, on obtient la relation bien connue :
4πR2σTe4= (1-A) πR2F0
où 4πR2 représente la surface de la terre, σTe4 l’émission du corps noir, (1-A) le coefficient d’absorption, πR2 la section de la terre, et F0 le flux solaire à l’extérieur de l’atmosphère ; Te est la température d’équilibre radiatif, A l’albédo planétaire, et σ la constante de Stefan-Boltzmann (5,67.10-8W.m-2 .K-4).
Pour quantifier l’effet du forçage radiatif sur la température moyenne globale, supposons dans un premier temps une atmosphère parfaitement transparente aux rayonnements thermiques réémis par la terre. Dans ce cas, la puissance radiative émise σTe4 équilibrerait exactement la puissance radiative incidente des radiations solaires de courte longueur d’onde atteignant effectivement la surface de la terre (1-A)F0/4, soit 240 W/m2 (F0 =1365,8 W/m2, l’albédo actuel est voisin de 0,3), ce qui donne Te=-18°C (255 K).
La température globale moyenne de la Terre est de 15 ° C (288 K), ce qui correspond à un pouvoir radiatif égal à σTe4 = 390 W/m2. La différence entre ce pouvoir radiatif et ce qui serait émis en l’absence d’atmosphère est de 390-240= 150 W/m2, ce qui correspond à l’absorption par l’atmosphère réelle en présence de vapeur d’eau, de gaz à effet de serre, de nuages et d’aérosols. L’efficacité du forçage radiatif est alors de (288-255)/150 = 0,22 °C/(W/m2).
Le réchauffement et le CO2 anthropique
Radiation thermique dans la bande d’absorption du CO2
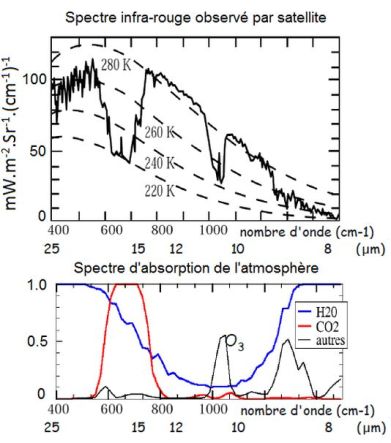
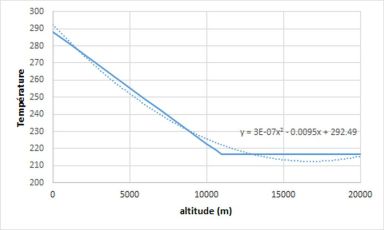
Connaissant l’efficacité du forçage radiatif, estimons l’impact sur la température globale d’une modification de la concentration du CO2 atmosphérique en faisant intervenir le rayonnement thermique dans la bande d’absorption du CO2 entre 630 et 700 cm-1. Lorsque la concentration augmente l’altitude à partir de laquelle le rayonnement thermique est émis vers le cosmos augmente également. Comme le montre le tableau représentant la pression partielle du CO2 (produit de la pression par la concentration) en fonction de l’altitude pour des concentrations de 300, 400 et 500 ppmv, la température du rayonnement émis peut être déterminée en utilisant les « température et pression normales » (TPN) qui permettent de s’affranchir des variations de ces deux paramètres selon le lieu et le temps considérés. La pression TPN est exprimée par la relation P=1013.25 x (1-0.0065 x z/288.15)5.255 où z est l’altitude (m). Au niveau de la mer la pression est de 1013,25 hPa, la température de 15 °C et le gradient thermique adiabatique de -6,5 °C/km. A 11 km d’altitude la pression a chuté à 226,38 hPa et la température à -56 °C. Entre 11 km et 20 km (stratosphère) la température reste constante. De manière à s’affranchir de la singularité de la température à 11000 m résultant du changement d’équation, un ajustement par un polynôme du second degré est opéré.
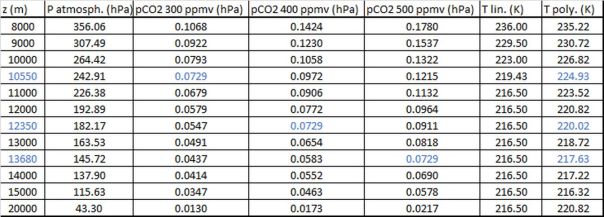
En considérant le rayonnement thermique qui correspond à 400 ppmv de CO2 , la puissance radiative émise déduite du spectre infrarouge observé par satellite, ramenée à la sphère terrestre, est 38,55/4=9,64 W/m2 pour une température égale à 220 K, ce qui correspond à une altitude de 12350 m et une pression partielle de CO2 de 0,0729 hPa.
On peut maintenant déduire quelle était la puissance radiative réémise au début de l’ère industrielle lorsque la concentration du CO2 était 300 ppmv, ce qui correspond à une altitude d’émission de 10550 m et une température de 224,93 K. L’application de la loi de Stefan-Boltzmann donne 9,64 x (224,93/220)4 = 10,53 W/m2, soit un gain de puissance de 10,53-9,64 = 0,89 W/m2. Ceci correspond à une diminution de la température de 0,19 °C d’après l’efficacité du forçage radiatif.
Pour ce qui est de l’impact climatique dans l’hypothèse du doublement de la concentration du CO2 anthropique, une concentration de 500 ppmv correspond à une altitude d’émission de 13680 m et une température de 217,63 K. La puissance radiative réémise déduite de la loi de Stefan-Boltzmann est 9,64 x (217.63/220)4 = 9,23 W/m2 soit une perte de puissance de 9,64-9,23 = -0,41 W/m2, ce qui correspond à une augmentation de la température de 0,09 °C.
Effet de l’élargissement de la bande d’absorption du CO2
Au réchauffement anthropique dû à l’augmentation de l’altitude à partir de laquelle le rayonnement thermique s’échappe vers le cosmos s’ajoute l’effet de l’élargissement de la raie d’absorption du CO2 lorsque la concentration en dioxyde de carbone croît. Si on considère une atmosphère d’humidité moyenne, l’augmentation, depuis le début de l’ère industrielle, du forçage radiatif ∆e (W/m2) résultant du rayonnement réémis vers la terre dans la bande 14 – 17 µm s’exprime en fonction de la teneur relative en CO2 par rapport à ce qu’elle était en 1850, soit (CO2)/(CO2)1850 , par la relation :
∆e=2.94*Log2 [(CO2)/(CO2)1850]
Le réchauffement anthropique déduit de la température globale instrumentale (Pinault, 2018e)
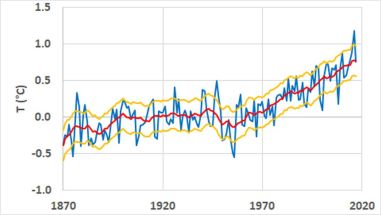
La contribution réelle du réchauffement anthropique au réchauffement total observé peut s’estimer de manière relativement précise en déduisant de la température globale instrumentale la variation naturelle de la température déduite de la mesure de la température de surface de la mer en des endroits précis des gyres subtropicaux représentatifs des échanges thermiques de longue durée entre les océans et les continents (voir « Changement climatique»).
La contribution anthropique à la température globale est obtenue en soustrayant le signal océanique de la température de surface instrumentale. Des variations significatives sont observées avant 1970, résultant principalement d’un manque de représentativité des zones sélectionnées pour estimer la contribution de chacun des océans à la variabilité du climat à partir de la température moyenne de la surface de l’eau de mer. La composante anthropique de la température globale a augmenté linéairement depuis 1970, sans aucune inflexion. Le réchauffement anthropique semble proche de 0,8 ° C en 2017.
Cette estimation est supérieure à l’augmentation de la Tmg résultant de l’augmentation de l’altitude à partir de laquelle le rayonnement thermique s’échappe vers le cosmos qui, elle, est voisine de 0.30 °C. Ce biais est principalement imputable à la couverture nuageuse de la haute troposphère, qui implique le gradient thermique adiabatique, l’albédo de surface et les rétroactions dues aux nuages. Le dioxyde de carbone contribue pour environ 80% au forçage radiatif dû aux gaz à effet de serre.
Références
Clive Best, Doubling CO2 and basic physics, http://clivebest.com/blog/?p=1169
Hanel R.A., B. Schlachman, D. Rogers, D. Vanous, The Numbus 4 Michelson interferometer, Appl Opt. 1971 Jun 1;10(6):1376-82. doi: 10.1364/AO.10.001376.
IPCC Fifth Assessment Report – Climate Change 2013 – www.ipcc.ch/report/ar5/wg1/
Dufresne J-L and Treiner J. (2011) L’effet de serre atmosphérique : plus subtil qu’on ne le croit !, http://www.udppc.asso.fr/bupdoc/consultation/article-bup.php?ID_fiche=21046 (in French)
Anthony Watts, The Logarithmic Effect of Carbon Dioxide, http://wattsupwiththat.com/2010/03/08/the-logarithmic-effect-of-carbon-dioxide/
ERBE (The Earth Radiation Budget Experiment) NASA program, 1996, FS-1996-05-03-LaRC, http://www.nasa.gov/centers/langley/news/factsheets/ERBE.html
Gill AE (1982) Atmosphere–Ocean Dynamics, International Geophysics Series, 30, Academic Press, 662 pp.
Kallberg, P., Berrisford, P., Hoskins, B., Simmons, A., Uppala, S. and Lamy-Thepaut, S (2005) ‘Atlas of the atmospheric general circulation’. ECMWF ERA-40 Project Report Series, No. 19. European Centre for Medium-Range Weather Forecasts, Shinfield, Reading, UK (available from www.ecmwf.int/publications)
Trenberth K. E., J. T. Fasullo, and J. Kiehl (2008) Earth’s Global Energy Budget, American Meteorological Society, DOI:10.1175/2008BAMS2634.1
Zhou, Y., D. P. Kratz, A. C. Wilber, S. K. Gupta, and R. D. Cess (2007), An improved algorithm for retrieving surface downwelling longwave radiation from satellite measurements, J. Geophys. Res., 112, D15102, doi:10.1029/2006JD008159.
Glossaire
La chaleur latente est la chaleur échangée lors du changement d’état de l’eau de mer au cours du processus de vaporisation.
Un corps noir en équilibre thermique (qui est à une température constante) émet un rayonnement électromagnétique appelé rayonnement du corps noir. Le rayonnement est émis selon la loi de Planck, ce qui signifie qu’il a un spectre qui est déterminé par la température seule, et non par la forme ou la composition du corps. Par exemple, le soleil peut être considéré comme émettant un rayonnement du corps noir qui présente une distribution en énergie caractéristique de la température T = 5780 K: la photosphère contient des photons presque en équilibre thermique, malgré leur évasion dans l’espace qui a un effet négligeable sur l’équilibre du rayonnement à l’intérieur de la photosphère.
Le rayonnement émis par la terre peut aussi être assimilé à l’émission d’un corps noir qui présente une distribution en énergie caractéristique de la température T=288K. Les photons dont l’énergie correspond aux bandes d’absorption saturées de l’atmosphère (vapeur d’eau, CO2) sont également en équilibre thermique s’ils s’échappent de la couche opaque : la température diminue progressivement avec l’altitude de la troposphère (-6,5°C/km).
L’albédo, qui est le rapport de l’énergie solaire réfléchie par une surface à l’énergie solaire incidente, est élevé sur les calottes polaires (de l’ordre de 60%) et beaucoup plus faible sur les océans (5 à 10%). Pendant une période de refroidissement les calottes polaires s’étendent, ce qui augmente l’albédo. La planète réfléchit davantage le rayonnement solaire, en absorbe moins, ce qui amplifie son refroidissement. Le réchauffement a des effets inverses: le réchauffement de la planète fait fondre la banquise polaire, ce qui diminue l’albédo et donc augmente la température de la planète.
Le gradient thermique adiabatique est, dans l’atmosphère terrestre, la variation de température de l’air avec l’altitude (autrement dit le gradient de la température de l’air). Adiabatique signifie qu’une masse d’air n’échange pas de chaleur avec son environnement (autres masses d’air, relief). Si l’on exclue la condensation (formation de nuages et précipitations) et la vaporisation, le gradient thermique de l’atmosphère ne dépend que de la pression.
Les bandes d’absorption du rayonnement infrarouge émis depuis la surface de la terre sont saturées lorsque la longueur optique est très inférieure à l’épaisseur de la couche absorbante de l’atmosphère. Dans ce cas, la couche est opaque et l’émission est réduite au rayonnement diffus (rayonnement thermique) depuis sa surface.
Bonjour
A propos de la valeur de 0,22 °C/( W/m2), voici ce qu’on peut observer, tous les 6 mois, sur chacun des 2 hémisphères (dont l’un, beaucoup plus océanique, montre des écarts saisonniers sur l’indicateur « température de surface en moyenne globale », 2 fois plus faibles):
https://e-nautia.com/arzi77/disk?p=5889169
La valeur de 0,56 °C/( W/m2), qui ressort de ces observations, (ou plutôt: de ces évidences), est inférieure à la valeur « à l’équilibre » que vous cherchez à déterminer (par des raisonnements, en effet, bien trop simples.)
Cette sous estimation est inévitable car, dans cette analogie que la nature nous permet d’établir (entre la Terre entière et l’un ou l’autre de ses hémisphères): il ne s’agit pas d’une augmentation permanente du forçage, liée à la modification en cours de la composition chimique de l’atmosphère, (elle conduira, dans quelques décennies ou siècles, à un nouvel équilibre) , mais d’une oscillation, (selon un rythme annuel), du forçage solaire.
Son amplitude est certes 10 ou 20 fois plus forte que la hausse du forçage par les GES, en raison de l’augmentation pérenne de leurs concentrations, mais sa variation rapide ne peut fournir qu’une valeur inférieure à celle qui sera observée au cours des prochains siècles.
J’espère que ces considérations vous conduiront à multiplier à nouveau par ~4 la valeur que vous calculez, ce qui fera disparaître tout fondement pour soutenir, ainsi que vous le faites, la thèse d’une surestimation de la gravité du transitoire en cours, irréversible à vue humaine.
J’aimeJ’aime
Merci, c’est en effet intéressant d’observer que votre valeur de 0,56 °C/(W/m2) est plus du double de celle obtenue à l’équilibre en raison de la variation saisonnière du gradient thermique adiabatique. Le raisonnement sur lequel je m’appuie ne correspond pas à un changement de climat entre un état initial et un état final mais à une modification virtuelle de la composition de l’atmosphère. Dans l’état initial l’atmosphère est transparente au rayonnement thermique alors que dans l’état final l’atmosphère est supposée à l’équilibre, ce changement d’état se faisant sans modification d’albédo. En première approximation la puissance radiative absorbée par les gaz à effet de serre augmente rapidement lorsque ces gaz sont peu concentrés alors que les bandes d’absorption de la vapeur d’eau et du CO2 ne sont pas encore saturées, puis tend à s’infléchir lorsque ces gaz se concentrent. C’est la raison pour laquelle je pense que la valeur 0,22 °C/(W/m2) est sur-estimée à l’équilibre, en raison de la non-linéarité.
J’aimeJ’aime
Bonjour, Je ne suis pas énergéticien mais la question de la responsabilité humaine dans le changement climatique ne me laisse pas indifférent. En effet la vapeur d’eau est de loin le GES majoritaire par rapport au CO2. Par ailleurs serait il possible de connaitre avec précision la proportion de CO2 anthropique par rapport au CO2 produit par la nature? De plus sachant qu’il existe d’autres GES disposant d’un potentiel de réchauffement global de loin plus important que le CO2 si bien que les efforts consentis pour réduire le CO2 anthropique sont comparable à la volonté d’assécher la mer par transvasement à l’aide d’un compte goute. Pourriez vous s’il vous plait m’apporter votre éclairage sur la question? Je vous remercie par avance.
J’aimeJ’aime
Bonjour, l’augmentation du CO2 depuis 1850, de l’ordre de 120 ppmv, est exclusivement imputable aux gaz de combustion. Elle est seulement responsable d’une partie du réchauffement, se superposant à la variabilité naturelle. Le CO2 est le principal gaz à effet de serre. Le méthane est beaucoup plus actif mais en plus faible teneur. Quant à l’eau, elle intervient peu dans les modifications du climat observées ces dernières décennies car sa concentration dans l’atmosphère varie peu. Elle augmente avec la température globale mais l’effet de serre qui en résulte (vapeur d’eau, nuages d’altitude) est compensé par l’effet d’albédo dû aux nuages bas.
Personnellement je m’oppose aux arguments catastrophistes du GIEC pour 2 raisons:
1) l’effet amplificateur sur le réchauffement dû à l’augmentation de la vapeur d’eau, supposé par le GIEC, n’existe pas (ou est très faible).
2) un phénomène de saturation de l’effet de serre apparaît lorsque la teneur en CO2 augmente, lorsque le rayonnement diffus s’échappe dans la stratosphère dont la température varie peu avec l’altitude.
Néanmoins l’augmentation des GES est préjudiciable, pour la part du réchauffement qui lui est imputable, mais aussi pour l’acidification des océans,…
J’aimeJ’aime
rene.bisaro@wanadoo.fr
Bonjour,
Deux fenêtres de transmission atmosphériques des IR existent: entre 8 et 12 µm et entre 3 et 5µm. Vous ne parlez pas de cette dernière pourtant elle laisse passer des rayonnements fortement énergétiques. Le CO2 absorbe -t- il ces rayonnements et cette absorption dépend elle de sa concentration?
Cordialement
R. Bisaro
J’aimeJ’aime
Bonjour,
Au-dessous de 8 µm l’atmosphère absorbe les rayonnements (bandes d’absorption de l’eau en particulier). En l’absence de rayonnement diffus, cette partie du spectre IR influe donc peu sur l’effet de serre.
Cordialement,
Jean-Louis Pinault
J’aimeJ’aime
Bonjour,
je continue de reunir informations, données, pour rediger un article expliquant ou se situe le probleme dans le debat entre les climato-croyants et les climato-sceptiques. j’avais besoin d’une derniere information concernant la question de saturation de l’effet de serre du CO2, et apres avoir lu quelques stupidités, dont certaines difficiles a detecter, je suis tombe sur votre article. je ne vois pas d’auteur, ni en haut ni en bas, mais en regardant les commentaires, j’ai l’impression que l’auteur est jean-Louis Pinault. je n’ai lu qu’une partie, qui m’a donne la reponse a ma question: saturation en premiere approximation, mais pour les ailes du spectre, l’energie captée augmente tout de meme avec la concentration. il me reste a verifier une information: l’energie dans l’IR mesurée par satellite serait quasi-nulle, ce qui validerait experimentalement cette saturation. Pourquoi les modeles ne la simulent t’ils pas reste un mystere. probablement une erreur dans le modele de transfert radiatif, car en faisant un modele simplifié analytique (fondé sur l’ETR), on retrouve cet effet. J’ecris ce commentaire surtout pour dire que je me suis arrete dans la lecture de cet article une fois obtenue ma reponse, mais en parcourant « a la molette de la souris » pour trouver l’auteur, j’ai remarque des elements de raisonnement, equations, graphiques, des ordres de grandeurs qui me font dire que si j’avais connu cet article 2 ans plus tot, j’aurais avancé beaucoup plus vite dans ce travail. je vais donc tout imprimer, lire tranquillement et comparer a mes propres conclusions et questions.
Cordialement,
— jean Barckicke —
J’aimeJ’aime
Bonjour,
Bien que la raie d’absorption du CO2 dans l’atmosphère soit saturée, le CO2 contribue néanmoins à l’effet de serre lorsque sa concentration augmente. Comme vous le rappelez, des IR s’échappent par les ailes de la raie. Mais, surtout, le rayonnement diffus s’échappe de la ‘bulle’ que forme le CO2 dans l’atmosphère. Or le diamètre de la ‘bulle’ augmente avec la concentration et sa température diminue.
J’aimeJ’aime
je suis vraiment « traînard »: je découvre ce site aujourd’hui, alors que la question de l’impact du CO2 me préoccupe depuis deux ans. Le parcours de l’article est à refaire, mais je retiens le résultat, l’accroissement de la concentration a un effet très faible sur la température. Ce qui confirme en somme la thèse de JM Bonnamy dans son livre récent: que pensez-vous de ce « pavé »? J’avais lu ce genre de résultat ailleurs, et je l’ai à tort attribué à un scientifique d’un grand Institut, il s’en est vexé. En résumé les conclusions me semblent de bon sens, mais j’ai le sentiment qu’on ne retrouve rien de tels dans les rapports du GIEC/IPCC: qu’en est-il vraiment? Je ne suis pas capable de pénétrer les méthodes et hypothèses qui sous tendent les résultats affichés dans la synthèse AR5.
Merci pour votre attention,cordialement.
J’aimeJ’aime
Merci pour votre intérêt. Dans le paragraphe « Le climat actuel » à la fin de la page:
https://climatorealiste.com/
vous verrez l’augmentation de la température depuis 1970 pour ce qui concerne la composante anthropique (a) et naturelle (b). La composante anthropique subit un effet d’amplification qui fait que certaines régions sont très impactées (Asie centrale,…). La rétroaction positive à l’origine de ce phénomène se situe probablement dans les couches supérieures de la troposphère (voir l’article).
Bien cordialement,
J’aimeJ’aime
Bonjour,
Bravo pour vos articles très instructifs.
J’aimerais connaitre votre avis, vos remarques au sujet de cet article:
http://www.science-climat-energie.be/2019/02/14/le-rechauffement-climatique-dorigine-anthropique/
Merci d’avance.
J’aimeJ’aime
Merci de vous intéresser à la question, je viens de répondre au blog que vous m’avez indiqué.
N’hésitez pas à me faire part de vos objections.
Bien cordialement,
Jean-Louis Pinault
J’aimeJ’aime
Merci pour votre site. Le site cité ci-dessus sert aux septiques du CO2 comme origine du réchauffement climatique. J’essaie de trouver un contre argument A un point développé par ce site: Il est développé que le CO2 ayant absorbé des IR de la Terre ne réémet pas d’IR mais retransmet l’énergie absorbée par contact avec les autres molécules environnantes et que donc il n’y a pas d’énergie rayonnée qui revient vers la Terre. (et sous entendu l’échauffement de l’atmosphère induit n’a pas le même effet que le rayonnement). Je ne connais pas et ne possède pas d’ouvrage ou des références sur les conditions d’émission d’un gaz dans l’IR. Merci de votre aide.
J’aimeJ’aime
J’ai vu merci bien.
Si je compile les informations, peut-on en conclure que le phénomène de back radiation directe du CO2 dans les basses couches de l’atmosphère est négligeable, mais qu’en revanche l’augmentation de sa concentration et le gonflement de la bulle autorise ce rayonnement à des altitudes plus élevées ou la température est plus faible. Ce rayonnement n’aurait à lui seul encore peu d’effet sur la température sans rétroactions positives.
Ai-je bien compris?
Vous dites que ce phénomène de rétroaction est mal connu. Vos recherches à ce sujet ne se rapprochent-elles pas de celles de Svensmark, de l’importance des nuages dans les thèses « solaristes » et notamment du projet CLOUD mené par le CERN ?
Merci d’avance pour le temps accordé à mes questions.
J’aimeJ’aime
Merci d’alimenter la discussion.
En effet l’augmentation de la teneur en CO2 dans l’atmosphère a un impact négligeable sur les basses couches de la troposphère en raison du phénomène de saturation de la raie d’absorption du CO2. Mais l’effet de serre résulte du rayonnement diffus (thermique) qui s’échappe de l’atmosphère vers l’espace à la limite de la zone opaque (zone pour laquelle tout rayonnement réémis par la terre dans la bande du CO2 est absorbé). Lorsque la concentration du CO2 augmente,, le rayon de la bulle opaque s’accroit.. Le rayonnement thermique s’échappant d’une enveloppe de plus en plus froide, c’est que davantage d’énergie thermique reste confinée à l’intérieur de la bulle (la température décroit avec l’altitude dans la troposphère).
C’est la raison pour laquelle l’effet de serre engendré par le CO2 est ridiculement faible comparé à celui du méthane dont la raie d’absorption n’est pas saturée. Mais la faible concentration de ce gaz fait que son impact est faible comparé à celui du CO2.
Pourtant l’augmentation de la température moyenne de surface de la terre depuis 1970, date à partir de laquelle la température instrumentale ne peut plus s’expliquer en faisant simplement intervenir les cycles naturels, montre que l’effet de serre résultant de l’échappement du rayonnement thermique subit un formidable effet d’amplification. La cause en est très mal connue. Beaucoup de climatologues pensent qu’elle est liée à l’augmentation de la vapeur d’eau dans l’atmosphère, induisant un effet de serre plus efficace. Cet enrichissement en vapeur d’eau résulterait de l’évaporation accrue des océans, ce qui induirait une rétroaction positive.
Mais la cartographie du réchauffement purement anthropique (débarrassé de la contribution naturelle) montre que la cause est ailleurs en raison de la forte disparité entre les régions, les océans jouant plutôt le rôle de modérateurs. Il faut alors faire intervenir le gradient thermique adiabatique pour expliquer cet effet d’amplification (effet de serre très puissant induit par les nuages dans les hautes couches de l’atmosphère).
On est très loin des tentatives d’explication basées sur l’impact du vent solaire sur le processus de nucléation des gouttelettes d’eau !
Bien cordialement,
Jean-Louis Pinault
J’aimeJ’aime
sur un post du 1er novembre 2015 il est indiqué des pouvoirs de réchauffement en °C/W/m², mais sur quelle durée?; on n’aura pas 0.5 °C en un an!!
de plus la température indiquée est la température de quoi? sachant qu’on ne connaît pas UNE température climatique, que la tempérzature qui ne doit pas croître de plus de 2° n’est pas une température physique mais un repère, un index
Cordialement
J’aimeJ’aime
Les variations de température du surface résultant du forçage solaire et orbital se font sur quelques décennies. Il s’agit de la température moyenne de surface de la terre. On la connait à partir de proxys (isotopes dans les carottes de glace ou de sédiments ayant un rôle intégrateur) pour le climat passé ou bien en moyennant les températures instrumentales (moyennes annuelles) à l’échelle de la planète pour le climat présent (depuis 1,5 siècle).
On observe un accroissement de la température moyenne de l’ordre de 0,8 à 1°C au cours des 70 dernières années. Ce réchauffement anthropique est très disparate: de l’ordre de 0,5°C en Europe de l’ouest, il peut atteindre 5°C au-delà du cercle polaire.
Si rien ne change quant à l’augmentation des gaz de combustion on peut penser que la température moyenne va continuer d’augmenter de l’ordre de 1°C au cours des 70 prochaines années, avec bien entendu de très grandes disparités géographiques.
Très cordialement,
Jean-Louis Pinault
J’aimeJ’aime
bonjour
pouvez vous m expliquer ce qu’est une bande d absortion et le fait qu elle soit saturée ou pas ? en m orientant vers un texte ou un cours pdf à télecharger?…merci s avance..
J’aimeJ’aime
Cette présentation peut vous être utile, au moins dans sa première moitié:
Cliquer pour accéder à m2pam_2012_jyg.pdf
Bonne journée,
Jean-Louis Pinault
J’aimeJ’aime
Bonjour, je suis un néophyte en matière d’effet de serre. J’aimerais donc, pour éclairer ma lanterne, poser quelques questions sur le fondement de votre article qui réside à mon avis au paragraphe « Radiation thermique dans la bande d’absorption du CO2 ».
1) Dans votre démonstration vous utilisez une température « ajustée » par un polynôme du second degré. Sur quelles mesures effectives ou quelles courbes théoriques repose cet ajustement ?
2) Je crois comprendre que la mesure de la puissance radiative est effectuée par un satellite géostationnaire qui gravite à 36000 km de l’équateur. Ce satellite perçoit la Terre comme un disque radiatif. Ce positionnement introduit une légère erreur sur le rayon du disque qui n’est pas égal à celui de la Terre (apparemment -2%). Ceci a-t-il une importance, sachant que les résultats de la démonstration indiquent des variations de flux thermiques et de températures très faibles ?
3) La puissance radiative de 38,55 W/m² est-elle celle mesurée par le satellite dans le domaine infrarouge ? Apparemment, le satellite ne mesure que le ¼ de la puissance rayonnée par la terre puisqu’il ne « voit » que la surface d’un disque radiatif et non celle de la sphère terrestre. Si la puissance de 38,55 W/m² est bien celle mesurée par le satellite doit-on la diviser ou bien la multiplier par 4 pour obtenir la puissance rayonnée par la Terre?
4) Pourquoi prendre comme référence pour les calculs d’altitude d’émission, une pression partielle de 0,0729 hPa quelle que soit la concentration du CO2 ?
Cordialement,
Robert BENZAKI
J’aimeJ’aime
Bonjour,
la part humaine de l’augmentation de CO2 dans l’atmosphere n’est pas contestable.
Par contre l’augmentation de la temperature moyenne de l’atmosphere me parait extrêmement difficile à mesurer .Mais enfin admettons.
Il semble probable que la part anthropique représente entre 30et 50% de cette augmentation. Il me parait essentiel d’identifier la part manquante.
mesurer .6 °c sur des plages de -50 à +50 °C me parait périlleux.
Si le solde d’augmentation est astronomique , comment a-t-il pu se révéler en seulement 200 ans , comme pour le petit âge glaciaire. Pas facile, le GIEC en parle-t-il? Rien dans Internet.
qu’en pensez-vous ?merci.
J’aimeJ’aime
Bonjour,
La part de l’augmentation de la température globale de surface attribuable aux gaz de combustion n’est pas facile à déterminer, en effet. pour 2 raisons:
1) la bande d’absorption du CO2 dans l’atmosphère est saturée ce qui fait que, en théorie, l’absorption du rayonnement thermique émis par la surface de la terre dans la bande 14 – 17 µm ne dépend pas de la concentration du CO2. C’est la hauteur d’émission du rayonnement thermique dans la haute atmosphère qui intervient.
2) la part du réchauffement attribuable à l’action directe des gaz à effet de serre est faible. L’essentiel du réchauffement provient de la contre-réaction positive de la vapeur d’eau sous l’effet des gaz à effet de serre.
Après quelques tergiversations des climatologues au début des années 2000 (le hiatus), un meilleur échantillonnage de la température terrestre a permis de consolider l’hypothèse de l’augmentation de l’ordre de 1°C/50 ans.
Jean-Louis
J’aimeJ’aime
Bonjour,
Merci pour cet article détaillé sur les mécanismes permettant au CO2 de continuer à intervenir en effet de serre malgré la saturation de sa bande d’absorption. Comme quoi, les mécanismes naturels sont bien complexes !
Mais il y a tout de même des ordres de grandeur qui continuent à me questionner : Si le CO2 anthropique est vraiment la cause du réchauffement actuel, comment expliquez-vous qu’autour de l’an 1000 il faisait plus chaud qu’aujourd’hui puisque les Vikings ont nommé Groenland (terre verte) la terre qu’ils venaient de coloniser ? En effet, on peut difficilement attribuer aux hommes de l’époque un niveau de CO2 capable d’un tel réchauffement…
Merci pour votre éclairage.
J’aimeJ’aime
Bonjour,
Le climat est en effet soumis à des variations naturelles sur lesquelles se superposent les effets d’origine anthropique. Au cours de l’Holocène (ces 12000 dernières années, période interglaciaire), le climat est dominé par une oscillation de période moyenne 768 ans (mode subharmonique 4 https://climatorealiste.com/modes-subharmoniques/) forcé en partie par les variations de l’irradiance solaire. D’amplitude très variable d’un cycle à l’autre, cette oscillation a atteint un maximum il y a environ 800 ans pendant lequel la température moyenne terrestre s’est élevée de 0.2 °C. Cette variation est faible si on la compare à l’élévation de température observée au cours de ces 50 dernières années, qui est de 1.2°C, mais elle s’est inscrite dans la durée, ce qui a suffi a faire fondre (très partiellement) la calotte polaire au sud du Groenland.
Le réchauffement imputable aux gaz à effet de serre est, quant à lui, très rapide.
Merci de vous intéresser à la question,
Jean-Louis
J’aimeJ’aime
Merci pour votre réponse… mais je reste sur ma faim.
En effet, comment pouvez-vous suggérer que le réchauffement naturel de l’an 1000 (moins que +0,2degrés puisque vous indiquez un maximum de +0.2degrés il y a 800ans soit 200ans après l’arrivée des Vikings au Groenland) soit inférieur à celui d’aujourd’hui (+1.2degrés) dit d’origine anthropique ? Comment croire que +0.2degrés, même sur le temps long, peut rendre le Groenland vert ? Alors qu’avec +1.2degrés depuis 50ans il est encore loin d’être redevenu vert…
Par ailleurs, si c’est un cycle naturel de période 800ans et que le dernier maximum a eu lieu il y a environ… 800ans, pourquoi donc ne serions-nous pas à proximité d’un nouveau maximum de ce cycle naturel ?
Bizarre, non ?
J’aimeJ’aime